It's important that you plan your flight around the winds; you want to get out in a certain area so that you can deploy your parachute in a certain area. But, well... as a skydiver, you often don't have control over that.
You get to trust the people giving the count, the people climbing out first. They are likely trusting the pilot, who is in turn trusting his instruments. On wingsuit or tracking jumps, you get to trust the leader to point you in the right direction. On the first load of the day, you get to trust the upper altitude wind forecasts.
Sometimes you end up in the wrong spot.
When and how can you get back?
Analysis
This problem boils down to comparing "how far can I fly?" versus how far you actually have to fly, so let's figure out what affects canopy flight.
First, let's define some variables:
- Initial altitude = $a$
- Glide angle = $\theta$
- Airspeed = $v$, representing the canopy's speed through the air
- Windspeed = $v_w$, representing the air's speed over the ground
Now let's make some assumptions for the purposes of this analysis:
- We assume the pilot is flying directly on the wind line.
- We assume the ground is flat.
- We assume that airspeed, windspeed, and glide angle are constant.
So: what is the pilot's maximum range?
Well, let's start by modeling canopy flight with a right triangle, relating airspeed $v$ and glide angle $\theta$ to horizontal speed $v_h$ and vertical speed $v_v$:
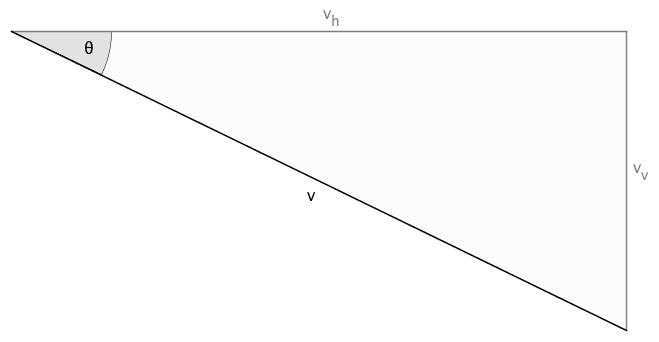
Trigonometry lets us define the vertical and horizontal speed components using our existing variables. SOH-CAH-TOA, anyone?
Now, let's make a couple more statements, substituting as we go:
Finally:
There's our answer! It's a doozy, but there's truths inside, so I'll unpack it for you.
Range is directly proportional to altitude.
This makes sense: if you could fly one mile from 2500', you'd be able to fly two miles from 5000' given the assumptions above. Put another way: pulling higher lets you fly further.
However, note that $v_w$ can be $< 0$, and if it's large enough, $range$ will be $< 0$. That is: a headwind can be strong enough that you'll lose ground no matter what. Since range is proprortional to altitude, in this scenario, pulling lower would help lose the least amount of ground.
The effects of wind are inversely proportional to airspeed.
The wind-related term above $\Bigl(csc(\theta)\frac{v_w}{v}\Bigr)$ is smaller if $v$ is higher and is bigger if $v$ is lower. We can re-state this as:
- Lower airspeed gives more range if the wind is pushing you the right direction. (Minimize $v$ when $v_w > 0$.)
- Higher airspeed gives more range if the wind is pushing you the wrong direction. (Maximize $v$ when $v_w < 0$.)
These follow even if we ignore horizontal airspeed entirely: speed is distance divided by time, so the faster you sink out of the wind, the less distance it will cause you to travel. If the wind adds to your range, you want to give it more time to do so; if it subtracts from your range, you want to give it less time.
Interestingly:
- Airspeed has no effect on range in the absence of wind. ($v$ disappears entirely when $v_w = 0$.)
This makes sense; wind is the only thing that adds a dependency on time. Without wind, range is a just function of glide angle and altitude.
Glide angle changes everything.
The keen observer will note that glide angle ($\theta$) factors into both the wind-dependent term and the wind-independent term. Any skydiver will also tell you that these parameters are interrelated; doing something to change the glide angle ($\theta$) will also change the airspeed ($v$).
Still, for reasonable values of $\theta$, $v$, and $v_w$, there are three basic rules of thumb to maximize range:
- Hold in deep brakes (greatly decreasing $v$) if the wind is significantly helping you.
- Hold front risers and reduce drag (greatly increasing $v$ and increasing $\theta$) if the wind is hurting you.
- Flatten your glide using rear risers (decreasing $\theta$) otherwise.
Math is hard. Let's go shopping!
Right?
The good news is, you don't need a calculator to figure out how to best recover from a bad spot. Or rather… you have one already.
Motion parallax allows us to use our movement through the sky as its own flight computer. This is very powerful, because now the math doesn't matter; physics will handle all the computations, you just need to understand how to read the results.
Your eyes can show you your current effective glide slope. In other words, assuming nothing changes (constant airspeed, constant windspeed, constant glide angle), your eyes can show you what line you will fly down and where you will land. This is sometimes called "the accuracy trick": find the spot on the ground that's not moving, and that's where you'll end up.
I consider this one of my basic flight instruments.
If my eyes can show me my glide slope, then I can experiment to find the configuration that gives me the most range.
Example
Say you open up and you're way out there. "Am I screwed?", you ask yourself. Well, find your glide slope, and make a note of where it appears to intersect the ground. If it's well past your target, hooray, you're probably not screwed. Otherwise, well, you probably are screwed after all.
If you're screwed, don't panic! Remember, all this assumes that things don't change, but you can change both your airspeed and glide angle with your normal flight controls. Also, wind speeds change with altitude – you remembered to check the winds aloft before boarding, right?
So, try something. Say, get on your rear risers a couple inches. How did the spot move? Did it move up? How much? All right. Now an inch more. It moved down? Okay, the first position gave you more range.
Try something else: brakes. Oh, that made the point move way down? You're probably facing into the wind. Try a little bit of fronts. That's better than rears? Great, stay there; this is your best option!
Wait, now the spot is moving down again, and a little to the left? Sounds like you dropped into different winds. Re-evaluate your airspeed and glide angle options until you find the best one again.
Of course, while you're doing this, you're also monitoring your altitude, evaluating alternative landing sites, and deciding to bail out as appropriate. You're also scanning the environment for anything that can give you information about wind at altitudes below you: chimneys, cooling towers, trees, flags, other canopies, anything. You're also making a note of where your friends are landing so you can help others locate them once you get down.
Calculator
You know, just in case:
| Altitude: | feet |
| Windspeed: | mph negative for headwind, positive for tailwind |
| Airspeed: | mph |
| Glide angle: | degrees |
| Range: |